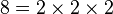Número é um objeto da Matemática usado para descrever quantidade, ordem ou medida. O conceito de número provavelmente foi um dos primeiros conceitos matemáticos assimilados pela humanidade no processo de contagem.
Para isto, os números naturais eram um bom começo. O trabalho dos matemáticos nos levou a descobrir outros tipos de números. Os números inteiros são uma extensão dos números naturais que incluem os números inteiros negativos. Os números racionais, por sua vez, incluem frações de inteiros. Os números reais são todos os números racionais mais os números irracionais.
Tipo de Números :
Números Naturais : Um número natural é um número inteiro não-negativo (0, 1, 2, 3, ...). Em alguns contextos, número natural é definido como um número inteiro positivo, i.e., o zero não é considerado como um número natural. Quando o símbolo dos números naturais (N) vier seguido de um asterisco (*) tira-se o 0 (zero).
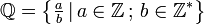 Lê-se Q igual a "a" sobre (ou dividido por) "b", tal que "a" pertence ao conjunto dos números inteiros e "b" pertence ao conjunto dos numeros inteiros não nulos. Onde
Lê-se Q igual a "a" sobre (ou dividido por) "b", tal que "a" pertence ao conjunto dos números inteiros e "b" pertence ao conjunto dos numeros inteiros não nulos. Onde  é o conjunto dos números inteiros e
é o conjunto dos números inteiros e  o conjunto dos números inteiros excluindo o 0.
o conjunto dos números inteiros excluindo o 0.
Tipo de Números :
Números Naturais : Um número natural é um número inteiro não-negativo (0, 1, 2, 3, ...). Em alguns contextos, número natural é definido como um número inteiro positivo, i.e., o zero não é considerado como um número natural. Quando o símbolo dos números naturais (N) vier seguido de um asterisco (*) tira-se o 0 (zero).
O uso mais comum deles é a contagem ("Há 4 quadros na parede") ou a ordenação ("Esta é a 2ª maior cidade do país"). Propriedades dos números naturais como, por exemplo, divisibilidade e a distribuição dos números primos, são estudadas na Teoria do Números. Propriedades que dizem respeito a contagens e combinações são estudadas pela combinatória.
Uma construção do conjunto dos número naturais que não depende do conjunto dos números inteiros foi desenvolvida por Giuseppe Peano no século XIX e costuma ser chamada de Axiomática de Peano
Números Inteiros : Os números inteiros são constituídos dos números naturais {0, 1, 2, 3, ...} e de seus simétricos {-1, -2, -3, ...}. Dois números são opostos se, e somente se, sua soma é zero. Por vezes, no ensino pré-universitário, chamam-se a estes números inteiros relativos.
O conjunto de todos os inteiros é denominado por Z (Mais apropriadamente, um Z em blackboard bold,  ), que vem do alemão Zahlen, que significa números, algarismos.
), que vem do alemão Zahlen, que significa números, algarismos.
 ), que vem do alemão Zahlen, que significa números, algarismos.
), que vem do alemão Zahlen, que significa números, algarismos.Os resultados das operações de soma, subtração e multiplicação entre dois inteiros são inteiros. Dois inteiros admitem relações binárias como =, > e <.
Matemáticos expressam o fato de que todas as leis usuais da aritmética são válidas nos inteiros dizendo que (Z, +, *) é um anel comutativo.
A ordem de Z é dada por ... < -2 < -1 < 0 < 1 < 2 < ... e faz de Z uma ordenação total sem limite superior ou inferior. Chama-se de inteiro positivo os inteiros maiores que zero; o próprio zero não é considerado um positivo. A ordem é compatível com as operações algébricas no seguinte sentido:
- se a < b e c < d, então a + c < b + d
- se a < b e 0 < c, então ac < bc
Como os números naturais, os inteiros formam um conjunto infinito contavel.
Os inteiros não formam um corpo, já que, por exemplo, não existe um inteiro x tal que 2x = 1. O menor corpo que contém os inteiros são os números racionais.
Uma importante propriedade dos inteiros é a divisão com resto: dados dois inteiros a e b com b ≠ 0, podemos sempre achar inteiros q e r tais que: a = bq + r e tal que 0 <= r < |b| (veja módulo ou valor absoluto). q é chamado o quociente e r, o resto da divisão de a por b. Os números q e r são unicamente determinados por a e b. Esta divisão torna possível o Algoritmo Euclidiano para calcular o máximo divisor comum, que também mostra que o máximo divisor comum entre dois inteiros pode ser escrito como a soma de múltiplos destes dois inteiros.
Tudo isto pode ser resumido dizendo-se que Z é um domínio euclidiano. Isto implica que Z é um domínio de ideal principal e que todo número inteiro podem ser escrito como produto de números primos de forma única (desde que o 1 não seja considerado primo).
Este é o teorema fundamental da aritmética.
O ramo da matemática que estuda os inteiros é chamado de teoria dos números.
Números Racionais :
Número racional é todo o número que pode ser representado por uma razão (ou fração) entre dois números inteiros.
O conjunto dos números racionais (representado por  , o uso da letra
, o uso da letra  é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
 , o uso da letra
, o uso da letra  é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por:
é derivada da palavra inglesa quotient, cujo significado é quociente, já que a forma de escrever um número racional é o quociente de dois números inteiros, com o denominador diferente de 0) é definido por: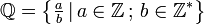 Lê-se Q igual a "a" sobre (ou dividido por) "b", tal que "a" pertence ao conjunto dos números inteiros e "b" pertence ao conjunto dos numeros inteiros não nulos. Onde
Lê-se Q igual a "a" sobre (ou dividido por) "b", tal que "a" pertence ao conjunto dos números inteiros e "b" pertence ao conjunto dos numeros inteiros não nulos. Onde  é o conjunto dos números inteiros e
é o conjunto dos números inteiros e  o conjunto dos números inteiros excluindo o 0.
o conjunto dos números inteiros excluindo o 0.Exemplos de números racionais:  ;
;  ;
; 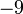 ;
; 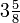 ;
; ![\,\!\sqrt[2]{4}](http://upload.wikimedia.org/math/e/a/0/ea0c7fb92d1298b193a5341ae8d140ae.png) ;
;  .
.
 ;
;  ;
; 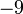 ;
; 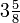 ;
; ![\,\!\sqrt[2]{4}](http://upload.wikimedia.org/math/e/a/0/ea0c7fb92d1298b193a5341ae8d140ae.png) ;
;  .
.Os números racionais opõem-se aos números irracionais ( ).
).
 ).
).Para representar o conjunto dos racionais positivos podemos usar Q + e para representar o conjunto dos números racionais negativos podemos utilizar Q-. O número zero também faz parte do conjunto dos racionais.
Há quatro formas de se apresentarem os números racionais: Frações (próprias ou impróprias), números mistos (que é uma variação das frações impróprias), números decimais de escrita finita e, por fim, as dízimas, que são números decimais em cuja escrita aparecem períodos numéricos infinitos. Eis alguns exemplos:
- Fração:
 ;
; - Número misto: 5
 ;
; - Números decimais de escrita finita: 8,35;
- Dízimas: 8,(23); 1,23(5); 7,23(965);
nesta notação os números entre parênteses repetem-se ao infinito.
Números Irracionais : Número irracional é um número real que não pode ser obtido pela divisão de dois números inteiros, ou seja, são números reais mas não não racionais. O conjunto dos números irracionais é representado pelo símbolo  .
.
 .
.Números Reais : O conjunto dos números reais 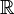 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
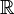 é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.
é uma expansão do conjunto dos números racionais que engloba não só os inteiros e os fracionários, positivos e negativos, mas também todos os números irracionais.Os números reais são números usados para representar uma quantidade contínua (incluindo o zero e os negativos). Pode-se pensar num número real como uma fracção decimal possivelmente infinita, como 3,141592(...). Os números reais têm uma correspondência biunívoca com os pontos de uma reta.
Denomina-se corpo dos números reais a colecção dos elementos pertencentes à conclusão dos racionais, formado pelo corpo de frações associado aos inteiros (números racionais) e a norma associada ao infinito.
Existem também outras conclusões dos racionais, uma para cada número primo, chamadas números p-ádicos. O corpo dos números p-ádicos é formado pelos racionais e a norma associada a p!
Número Primo : Um número natural é um número primo quando ele tem exatamente dois divisores: o número um e ele mesmo[1].
Nos inteiros,  é um primo se ele tem exatamente quatro divisores:
é um primo se ele tem exatamente quatro divisores: 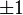 e
e 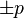 . Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
. Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
 é um primo se ele tem exatamente quatro divisores:
é um primo se ele tem exatamente quatro divisores: 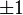 e
e 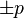 . Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.
. Uma definição um pouco mais técnica, que permite generalizar este conceito para outros conjuntos, é dizer que o conjunto dos divisores de p que não são inversíveis não é vazio, e todos seus elementos são produtos de p por inteiros inversíveis. Por definição, 0, 1 e − 1 não são números primos.A propriedade de ser um primo é chamada "primalidade", e a palavra "primo" também é utilizada como substantivo ou adjetivo. Como "dois" é o único número primo par, o termo "primo ímpar" refere-se a todo primo maior do que dois.
Se um número inteiro tem módulo maior que um e não é primo, diz-se que é composto. Por convenção, os números 0, 1 e -1 não são considerados primos nem compostos.
O conceito de número primo é muito importante na teoria dos números. Um dos resultados da teoria dos números é o Teorema Fundamental da Aritmética, que afirma que qualquer número natural diferente de 1 pode ser escrito de forma única (desconsiderando a ordem) como um produto de números primos (chamados fatores primos): este processo se chama decomposição em fatores primos (fatoração).
Os 100 primeiros números primos positivos são:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541
Exemplos de decomposições: